R. Condit
Nico Lubcker and colleagues made measurements of southern elephant whiskers, including multiple measurements of individual whiskers over one year. They are essentially identical to measurements from Burnyce, the captive northern elephant seal (Beltran et al. 2015), and Roxanne Beltran organized Nico's data. The goal here is to fit a growth curve to individual whiskers, as we did for Burnyce's whiskers. Any whisker with 3 or 4 measurements allows a precise fit of the Von Bertalanffy growth model.
Since whiskers were cut at the skin at the time of the first measurement, there are two alternate ways of fitting the model, 1) either with the reduced size, which starts at zero, or 2) using the original size, a description of the whisker size had it never been cut. The difference between the two is simply a constant length subtracted from the original size. I show first that there is a very simple relationship between the resulting von Bertalanffy curves from full and reduced sizes.
Invariance of von Bertalanffy to a transformation
Imagine any object whose size measurements at time t, \( S_t \), follow a von Bertalanffy curve, \( S_t = A(1-e^{-k(t-T_o)}) \label{vonB} \).
- \( A = S_\infty = \) Asymptotic size
- \( T_o = \) Initial time, when growth begins and \( S = 0 \)
- \( k = \) A curvature constant describing how quickly S approaches A
At any time \( T_b \), when the size is \( S_b \), the object is cut back to size zero, then continues to grow as if it were never cut (as Ibrahim and Wright 1978 found for mouse whiskers).
- \( T_b = \) Time of cutting back to size zero
- \( S_b = \) The size prior to cutting at \( T_b \), which is just the amount cut off
Define a new coordinate system, \( t'=t-T_b \) and a new size, \( S'=S-S_b \). With some straightforward algebraic manipulation, it turns out that \begin{equation} S' = (A-S_b)(1-e^{-kt'}). \end{equation} This is also a von Bertalanffy curve, with identical \( k \) and an asymptote \( A-S_b \), the old asymptote minus what was cut off. This means that a von Bertalanffy model could be fit to either the full sized whisker (size \( S \)) or the smaller whisker (size \( S-S_b \)), and both will yield the same \( k \).
Fitting von Bertalanffy to whiskers with 3 or more measurements
Roxanne prepared two files, 'SESE Whisker Data_PartialSet.csv' and 'SESE Whisker Data_FullSet.csv', the first with whiskers measured only twice, the second having 3 or more measurements; the csv files are identified by R names NicoDataFile1 and NicoDataFile2 below. I use an R function whiskerdataSES to read and rearrange the tables of data (all R functions are in a here). The new R dataframe, called sew, includes the Length as Nico measured (after cutting), and the LengthOrig, the length had the whisker not been cut (assuming unchanged growth).
library(xtable) source('whiskerSES.r')
NicoDataFile1
[1] "SESE Whisker Data_PartialSet.csv"
NicoDataFile2
[1] "SESE Whisker Data_FullSet.csv"
bestSESWhisker=whiskerdataSES(infile=NicoDataFile2,minTime=200) head(bestSESWhisker)
Tag Time Length MeasurementType CutPart LengthOrig 1 YO059 0 0 t0 66 66 2 YO059 23 11 t1 66 77 3 YO059 43 19 t2 66 85 4 YO059 392 58 t3 66 124 6 YO064 0 0 t0 77 77 7 YO064 34 19 t1 77 96
The function fitWhiskerHier provides a Bayesian fit to a hierarchical model, where each individual seal is treated as a random effect. The hierarchical model provides a direct measure of variation across individuals and strong estimates of confidence intervals. Still, I use only those 19 animals with 3 measurements spanning at least 200 days, since evidence on growth rate (decelerating or not) requires 3 data points.
I tested a model in which the residual SD (the error around the model) increased with whisker size, but results were not satisfying. The model chose a high error in large whiskers, and essentially no variation between seals. It seems more likely on a priori that error would not change with whisker size, and the model with constant SD produced variation between seals. I also realized that a model in which T0 is fixed at 0 is better, since we know whiskers were cut to size 0 at the start. In all cases, I transformed the curvature parameter to log(k), since that allowed a Gaussian hyper-distribution (otherwise, the variance in k would not be Gaussian, since k must be > 0).
whiskerHierModel=fitWhiskerHier(w=bestSESWhisker,fitcol='Length',iter=25000,show=50,burn=5000, startsd=2,SDmodel=constant,startpar=c(T0=0,k=(-4.4),A=120)) whiskerHierModel2=fitWhiskerHier(w=bestSESWhisker,fitcol='Length',iter=25000,show=50,burn=5000, startsd=2,gmodel=vonBertanlanffy.lmer0,startpar=c(k=(-4.4),A=120), SDmodel=constant,badVB=badVonB0param) test=fitWhiskerHier(w=bestSESWhisker,fitcol='Length',iter=25000,show=50,burn=5000, startsd=c(2,0),SDmodel=linear.model,startpar=c(T0=0,k=(-4.4),A=120)) save(whiskerHierModel2,file=pst(whiskerpath,'whiskerHierModel_best.rdata'))
[1] 3
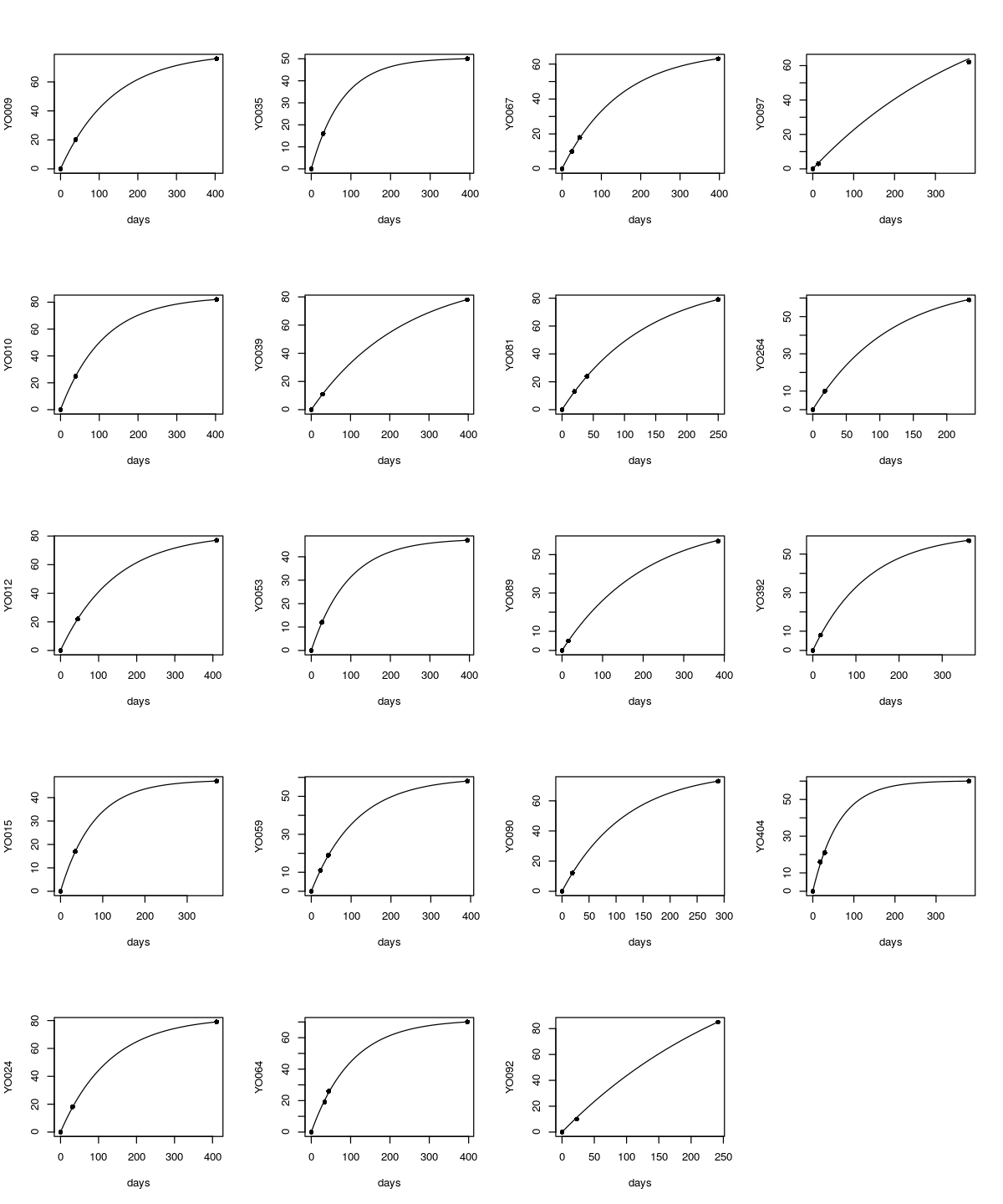
Fitted parameters for 19 seals based on whiskerHierModel2. The final row is the fixed effect, the parameters for the entire set of 19 seals.
print(xtable(tableWhiskerHier(fit=whiskerHierModel2,useLogK=TRUE)[[1]]),type='html')
| K_CI | Asymptote_CI | GrowthDay0 | GrowthDay40 | Max | Cut | |
|---|---|---|---|---|---|---|
| YO009 | 0.00736 (0.0068,0.0080) | 80.1 (78.4,81.9) | 0.590 (0.55,0.63) | 0.439 (0.42,0.46) | 76.00 | 82.00 |
| YO010 | 0.00899 (0.0084,0.0096) | 84.3 (82.8,85.7) | 0.758 (0.72,0.80) | 0.529 (0.51,0.55) | 82.00 | 94.00 |
| YO012 | 0.00696 (0.0064,0.0075) | 81.7 (79.8,83.7) | 0.569 (0.53,0.61) | 0.430 (0.41,0.45) | 77.00 | 64.00 |
| YO015 | 0.01260 (0.0114,0.0138) | 47.5 (46.2,48.8) | 0.598 (0.54,0.65) | 0.361 (0.34,0.38) | 47.00 | 71.00 |
| YO024 | 0.00767 (0.0070,0.0084) | 82.6 (80.8,84.4) | 0.636 (0.59,0.68) | 0.466 (0.44,0.49) | 79.00 | 81.00 |
| YO035 | 0.01269 (0.0115,0.0140) | 50.4 (49.1,51.6) | 0.639 (0.59,0.70) | 0.385 (0.37,0.40) | 50.00 | 54.00 |
| YO039 | 0.00420 (0.0034,0.0049) | 96.3 (90.1,104.9) | 0.405 (0.36,0.45) | 0.342 (0.32,0.37) | 78.00 | 80.00 |
| YO053 | 0.01070 (0.0094,0.0120) | 47.7 (46.5,49.1) | 0.511 (0.45,0.57) | 0.333 (0.31,0.35) | 47.00 | 68.00 |
| YO059 | 0.00885 (0.0082,0.0095) | 59.9 (58.5,61.4) | 0.531 (0.50,0.57) | 0.373 (0.36,0.39) | 58.00 | 66.00 |
| YO064 | 0.00975 (0.0092,0.0103) | 71.5 (70.2,72.9) | 0.698 (0.67,0.73) | 0.472 (0.46,0.49) | 70.00 | 77.00 |
| YO067 | 0.00668 (0.0061,0.0073) | 67.9 (66.0,69.9) | 0.453 (0.42,0.48) | 0.347 (0.33,0.36) | 63.00 | 80.00 |
| YO081 | 0.00739 (0.0067,0.0080) | 93.8 (90.6,98.1) | 0.693 (0.65,0.73) | 0.516 (0.50,0.53) | 79.00 | 72.00 |
| YO089 | 0.00482 (0.0035,0.0066) | 68.1 (61.6,77.5) | 0.332 (0.27,0.41) | 0.270 (0.23,0.32) | 57.00 | 61.00 |
| YO090 | 0.00845 (0.0071,0.0098) | 80.1 (77.1,84.0) | 0.676 (0.59,0.76) | 0.482 (0.45,0.51) | 73.00 | 77.00 |
| YO092 | 0.00332 (0.0027,0.0043) | 154.3 (131.3,177.7) | 0.511 (0.48,0.57) | 0.447 (0.43,0.47) | 85.00 | 82.00 |
| YO097 | 0.00236 (0.0015,0.0047) | 107.7 (74.1,145.6) | 0.253 (0.21,0.34) | 0.227 (0.20,0.29) | 62.00 | 86.00 |
| YO264 | 0.00860 (0.0068,0.0102) | 68.4 (64.6,74.3) | 0.590 (0.51,0.66) | 0.416 (0.39,0.44) | 59.00 | 83.00 |
| YO392 | 0.00774 (0.0064,0.0093) | 60.9 (58.5,63.9) | 0.471 (0.40,0.54) | 0.346 (0.31,0.38) | 57.00 | 80.50 |
| YO404 | 0.01557 (0.0146,0.0166) | 60.2 (59.0,61.4) | 0.936 (0.88,0.99) | 0.502 (0.49,0.51) | 60.00 | 79.00 |
| Fixed_effect | 0.00744 (0.0058,0.0095) | 77.1 (65.4,89.9) | 0.573 (0.48,0.68) | 0.424 (0.37,0.48) |
| \( T_o \) | Time at size 0, when whisker erupted through skin (in days) |
| \( K_CI \) | Curvature constant with 95% credible intervals (units are \( day^{-1} \) |
| \( A_CI \) | Asymptote with 95% credible intervals (mm) |
| \( GrowDay0 \) | Growth rate at \( t=0 \), which is maximum growth ( \( mm \cdot d^{-1} \) ), with 95% credible intervals |
| \( GrowDay40 \) | Growth rate at \( t=40 \), with 95% credible intervals |
| \( Max \) | Maximum measured size (mm) |
| \( Cut \) | Length of whisker cut off before experiment started (mm) |
In YO097, the fitted \( A \) and \( k \) are well out of range, probably having to do with the short time between the first two measurements, presumably adding error to \( k \). Otherwise, the estimated parameters resemble those from Burnyce reasonably well. If this model were fitted to the reduced whisker size, those measurements after cutting, the resulting \( k \)'s would be identical, and the resulting \( A \)'s would be lower by exactly the amount cut. With that method, however, \( T_o \) would not be estimated.
Graphs of the model fits for all 19 animals.
graphWhiskerHier(fit=whiskerHierModel2,gmodel=vonBertanlanffy.lmer0)
Methods for manuscript
Our starting assumption was that whisker growth in the post-weaned animals was asymptotic, based especially on detailed measurements of many whiskers in a northern elephant seal (Beltran et al. 2015). In that case, whisker growth rate was always decelerating, and size reached an asymptote after about one year. That animal, however, was a full-sized adult, and ours were growing juveniles. Nevertheless, in the 19 animals for which we had three or more whisker measurements over a year, growth rate clearly decelerated, and relative growth in body size over the year post-weaning is small compared to relative growth in whisker size. We thus held the assumption that the Von Bertalanffy asymptotic growth model was our best option. Given decelerating growth, we need at least three measurements to fit properly, so we used only those 19 cases.
We fitted the Von Bertalanffy model to length of all 19 animals' whiskers jointly, treating individual seal as a random effect (equivalent to repeated measures). The model is thus specified
\begin{equation} \DeclareMathOperator{\dnorm}{dnorm} \DeclareMathOperator{\vonb}{VonB} \DeclareMathOperator{\mean}{mean} \DeclareMathOperator{\sd}{sd} size \sim \vonb(time + time|seal) + \epsilon \label{E1} \end{equation}indicating that size was modeled as a function of time using the Von Bertalanffy function, with seal as a random effect, and a normally-distributed error \( \epsilon \). The general Von Bertalanffy function is
\begin{equation} S_p(A,k,T_0) = A (1 - e^{-K(t-T_0)}) \label{E2} \end{equation}where \( S_p \) means predicted size given three parameters: \( A \), asymptotic size; \( k>0 \), the curvature parameter; and \( T_0 \), the time at which growth begins (so \(S_p = 0 \)). Since we cut whiskers to the skin, we can set \( T_0 = 0 \) and estimate only \( K \) and \( A \). The model parameters include a fixed effect \( \theta_F = (A_F,K_F \)), the best estimate for all 19 animals together, plus a separate set of parameters \( \theta_i = (A_i,K_i)\) for each animal \(i\). There must be a hyperdistribution for \( \theta_i \), describing the variance between animals, which we assumed to be bivariate Gaussian. To allow the Gaussian assumption, a parameter transformation was necessary, using \( L = \log(K) \), since a Gaussian distribution for \( L_i \) is reasonable but not for \(K_i\), which is always a very small positive number. In fact, then, model parameters were \( L \) and \( A \), but we always back-transformed in presenting results and never display \( L \). The asymptote \( A \) was also constrained to be > 0, however it never approached 0 so the Gaussian hyper-distribution worked well. One additional parameter needed for the model was \( \epsilon \), or the residual standard deviation of the error around the model, again assumed to be Gaussian.
Estimating parameters required one likelihood function for the observations, describing the probability \( P_{ij} \) of measuring seal \( i \)'s whisker on day \( j \) as size \( S_{ij} \), given predicted size \( S_p \) based on the model and parameters \( \theta_i \) for seal \( i \), plus the residual Gaussian error,
\begin{equation} P_{ij} = \dnorm( S_{ij}, \mean=S_p(\theta_i), \sd=\epsilon), \label{E3} \end{equation}where dnorm is the standard normal deviate given the mean and standard deviation sd. Equation \eqref{E3} must be repeated for every measurement of every seal \(i\), and the log-likelihood of all observations is \( \sum_{ij}{\log P_{ij}} \).
There are two additional likelihood function for the fixed effects, \( \theta_F \),
\begin{align} P_{Ai} &= \dnorm( A_i, \mean=A_f, \sd=\sigma_A) \nonumber \\ P_{Li} &= \dnorm( A_i, \mean=L_f, \sd=\sigma_L) \label{E4} \end{align}where \( A_f \) and \(\sigma_A\) area hyper-mean and hyper-standard-deviation of 19 whiskers' asymptote sizes, and likewise for hyper-mean and hyper-SD of \( L_f = log(K_f)\). The log of the two probabilitities in Equation \eqref{E4} must be summed over each animal \(i\). The total log-likelihood for the entire set of observations, given an entire set of parameters \(\theta_i\) and \( \theta_F\), is
\begin{equation} \Pi = \sum_{i}{\log P_{Ai}}+\sum_{i}{\log P_{Li}}+\sum_{ij}{\log P_{ij}}. \label{E5} \end{equation}Parameters were estimated in a Bayesian framework, using Metropolis updates based on the full likelihood formulation (Eq. \eqref{E5}). The entire set of parameters were updated 25000, and the first 5000 discarded as burn-in. The remaining 20000 values describe posterior distributions for every parameter. Credible intervals (95%) for each were defined as the central 95 percentiles of these distributions. The individual parameters A_i and K_i were used to describe growth trajectories for all 19 seals' whiskers. In addition, given the Von Bertalanffy formulation, with \(T_0=0\), whisker growth rate at time \(t\) can be calculated as
\begin{equation} G_t = A k e^{-kt}. \label{E7} \end{equation}Posterior distributions of \( A_i \) and \( K_i \) were converted into posterior distribution of growth rates at day 0 and day 40 for each seal, with associated 95% credible intervals.
Appendix: Early results
I originally experimented by fitting data to those same 19 whiskers in a non-hierarchical model based on R's function option. My function fitAllWhiskerOptim fits the model for each of the whiskers in NicoDataFile2, those with 3 measurements, and graphs the resulting models. It also returns a table of fitted parameters. In the example below, the model is fitted to the original, larger, whisker length (it could just as easily be fitted to the cut Length by setting ycol='Length'). The following code is not executed, though, in favor of the hierarchical model above.
par(mfcol=c(1,4),mai=c(.75,.75,0,0),mgp=c(2,1,0)) fitAllWhiskerOptim(input=bestSESWhisker,ycol='Length',graphit=TRUE)
fitAllWhiskerOptim(input=bestSESWhisker,ycol='LengthOrig',graphit=FALSE)